1. Qu’est-ce que Wireguard ?
Wireguard est un protocole de communication, ainsi qu’un logiciel, permettant de créer un VPN. C’est un logiciel libre et open-source. Il a pour objectif d’être plus rapide et plus simple que les autres solutions notamment IPsec. Il a également pour ambition d’être considérablement plus performant que OpenVPN.
2. Installation Wireguard
Présentation
L’objectif de ce lab. sera de mettre en place un serveur Wireguard, pour permettre à des utilisateurs extérieurs de se connecter à un réseau interne, non disponible depuis l’extérieur.
Pour cela :
Serveur :
– Debian 11
– 2 Interfaces réseau (une accessible de l’extérieur l’autre uniquement accessible en interne) et un tunnel Wireguard.
– enp0s3 :
– IP : 10.188.80.31 /16
– Réseau : 10.188.0.0
– Accessible depuis l’extérieur
– enp0s8 :
– IP : 192.168.1.1/24
– Réseau : 192.168.5.0
– Réseau interne
– wg0 Serveur :
– IP : 192.168.5.1/24
– Réseau : 192.168.5.0/24
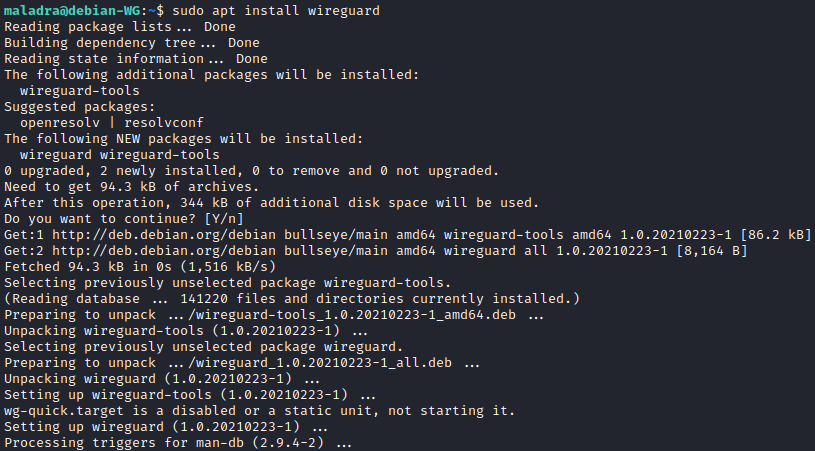
Pour l’installation de Wireguard sur Debian, il suffit d’effectuer la commande :
sudo apt install wireguard
Cette commande est à effectuer sur le serveur et sur le client, afin d’installer Wireguard.
3. Génération des couples de clés
Pour commencer il faut générer un ensemble de clés privée/publique sur le serveur pour cela :
wg genkey > private
wg pubkey < private > public

La clé privée comme son nom l’indique, doit rester privée. Elle ne doit pas être partagée et doit rester uniquement sur le serveur. La clé publique a pour vocation d’être partagée aux différents Peer et leur permettra de se connecter au VPN. Enfin pour générer les clés sur le client il suffira d’effectuer les mêmes manipulations que sur le serveur.
4. Configuration Wireguard Serveur
Pour la configuration du Wireguard tout se passe dans le dossier /etc/wireguard/ aussi bien pour le serveur que pour le client. Chaque interface aura son propre fichier de configuration. Donc par exemple une première configuration dans le fichier wg0.conf, une deuxième configuration dans le fichier wg1.conf, etc.
Nous allons commencer par configuer le serveur pour ce faire :
sudo nano /etc/wireguard/wg0.conf
Configuration de l’interface :
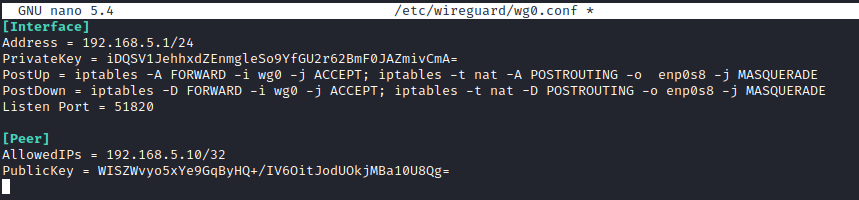
Address : Représente l’adresse IP, ainsi que le masque de l’interface du Wireguard
PrivateKey : Représente la clé privée du serveur
PostUp : Représente les commandes iptables effectuées au moment de l’activation de l’interface
PostDown : Représente les commandes iptables effectuées au moment de la désactivation de l’interface
Listen Port : Représente le port sur le quel Wireguard est en écoute
Configuration du Peer :
AllowedIPs : Dans ce cas autorise les paquets ayant pour IP source l’IP spécifiée
PublicKey : Représente la clé publique du client générée précédemment
A noter que pour chaque client du VPN, il sera nécessaire de déclarer un nouveau Peer dans le fichier de configuration.
IP Masquerade
Pour permettre à notre serveur d’effectuer du routing, il faut donc les deux règles iptables dans la configuration du Wireguard. Mais en plus de cela il faut autoriser le routing des paquets. Pour ce faire il faut modifier le fichier /etc/sysctl.conf avec la commande suivante :
sudo sysctl -w net.ipv4.ip_forward=1

5. Configuration Wireguard client
Enfin pour la configuration du client le chemin d’accès sera exactement le même que celui du serveur : /etc/wireguard/wg0.conf
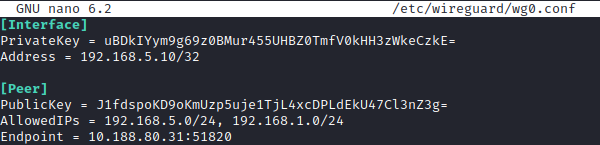
Configuration de l’interface :
PrivateKey : Représente la clé privée du client générée précédemment
Address : Représente l’adresse IP que prendra l’interface une fois activée
Configuration du Peer :
PublicKey : Représente la clé publique du serveur
AllowedIPs : Dans ce cas indique les réseaux joignables par l’interface
Endpoint : Indique l’adresse à contacter pour se connecter au Wireguard
6. Activation des interfaces
Il ne reste plus qu’à activer l’interface sur le serveur ainsi que sur le client pour ce faire :
sudo wg-quick up wg0

* Activation de l’interface sur le serveur
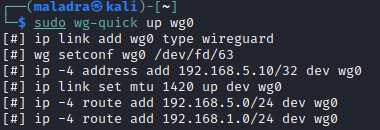
* Activation de l’interface sur le client
7. Résultat
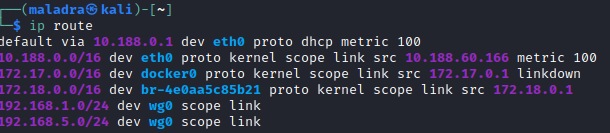
Comme nous pouvons le voir sur la capture d’écran suivante, les réseaux 192.168.1.0/24 et 192.168.5.0/24, sont bien accessible par l’interface wg0 du client.
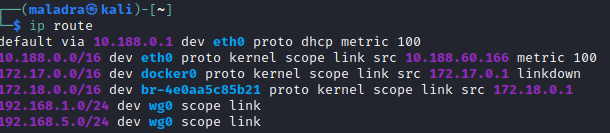
Il est donc également possible de vérifier cela avec la commande ping, en effectuant un ping depuis notre machine cliente vers l’interface 192.168.1.1 du serveur, qui n’est pas accessible depuis l’extérieur.
8. Commandes supplémentaires
Activation de l’interface à chaque redémarrage de la machine
Par défaut l’interface ne s’active pas au démarrage. Pour le permettre il faut l’activer avec systemctl.
sudo systemctl enable wg-quick@wg0

Vérifier l’état du tunnel Wireguard
Permet de vérifier l’état du tunnel, la quantité de données transférées, les clients connectés.
sudo wg show wg0
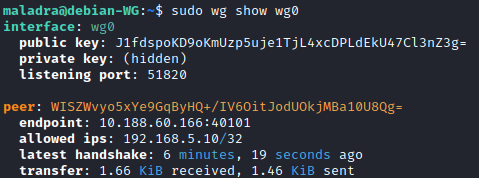
Désactivation du tunnel Wireguard
Permet de désactiver le tunnel Wireguard.
sudo wg-quick down wg0